KALKULUS 2 FORUM DISKUSI 16 : VOLUME BENDA PUTAR
PENGERTIAN VOLUME BENDA PUTAR
volume benda putar adalah volume yang diperoleh dari sebuah luasan yang diputar dengan poros putar tertentu (sumbu x atau sumbu y). Contoh paling sederhana dari benda putar yaitu pada sebuah tabung. Volume sebuah tabung diperoleh dari luas alas berbentuk lingkaran yang dikalikan dengan tinggi.
Apabila alas sebuah tabung dinyatakan dengan fungsi A(x) dan tinggi dari benda putar tersebut yaitu panjang selang dari titik a ke b pada sumbu x atau y, maka volume pada benda putar tersebut bisa dihitung dengan menggunakan rumus :
V = ∫ba A(x) dx
JENIS METODE MENENTUKAN VOLUME BENDA PUTAR
Suatu daerah jika di putar mengelilingi garis tertentu sejauh 360º, maka akan terbentuk suatu benda putar. Kegiatan pokok dalam menghitung volume benda putar dengan integral adalah: partisi, aproksimasi, penjumlahan, pengambilan limit, dan menyatakan dalam integral tentu.
Dalam menentukan volume benda putar yang harus diperhatikan adalah bagaimana bentuk sebuah partisi jika diputar. Berdasarkan bentuk partisi tersebut, maka metode yang digunakan untuk menentukan volume benda putar adalah metode cakram, metode cincin, dan metode kulit tabung yang selanjutnya dihitung dengan menggunakan integral tentu.
Menghitung volume benda putar dengan menggunakan metode cincin dilakukan dengan memanfaatkan rumus volume cincin seperti gambar di bawah, yaitu
V = π(R2 - r2)h
Gambar Metode Cincin
RUMUS VOLUME BENDA PUTAR DENGAN METODE CAKRAM
Misalkan kurva y = f(x) dari 0 sampai a dipotong-potong dalam bentuk cakram sebagaimana diilustrasikan dengan gambar di bawah ini. Bentuk cakram di bawah dapat dianggap sebagai tabung dengan jari-jari r = f(x), tinggi h = Δx. Sehingga volumenya dapat diaproksimasi sebagai
ΔV ≈ π r2 h atau ΔV ≈ π f(x)2 Δx.
Dengan cara menjumlahkan, mengambil limitnya, dan menyatakan dalam integral diperoleh:
V ≈ Σ π f(x)2 Δx
V = lim Σ π f(x)2 Δx
V = π 0∫a [ƒ(x)]2dx atau V = π 0∫a y2dx
Gambar Metode Cakram
MENENTUKAN VOLUME BENDA PUTAR DENGAN METODE KULIT TABUNG
Metode kulit tabung secara matematis dapat diilustrasikan sebagaimana gambar di bawah.



Gambar Metode Kulit Tabung
Gambar Metode Kulit Tabung
Secara umum apabila daerah yang dibatasi oleh kurva y=f(x) dan y=g(x) dengan |f(x)| > |g(x)| pada interval [a, b] diputar mengelilingi sumbu-X, maka volume benda putar yang diperoleh dapat ditentukan dengan menggunakan integral tentu sebagai berikut:
Secara grafis dapat diilustrasikan sebagai berikut :

Volume Benda Putar yang Dibatasi Dua Kurva Jika Diputar Mengelilingi Sumbu y
ilustrasi benda putar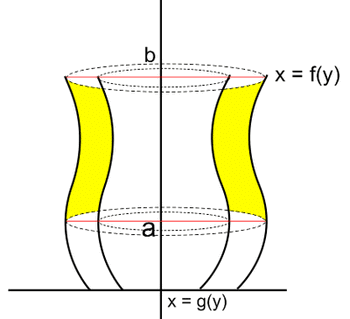
Prinsipnya sama dengan yang ada di huruf b, apabila terdapat sebuah luas yang terbentuk dari dua buah kurva x = f(y) dan x = g(y) dan interval [a.b] yang diputar mengitari sumbu y maka volume yang dihasilkan bisa dicari menggunakan rumus berikut :
Volume Benda Putar yang Dibatasi Dua Kurva Jika Diputar Mengelilingi Sumbu x
Jika terdapat sebuah luasan yang dibatasi oleh dua kurva yaitu f(x) dan g(x) dimana |f(x)| ≥ |g(x)| dengan interval [a,b] diputar mengelilingi sumbu x, maka volume benda putar tersebut bisa dihitung
menggunakan rumus: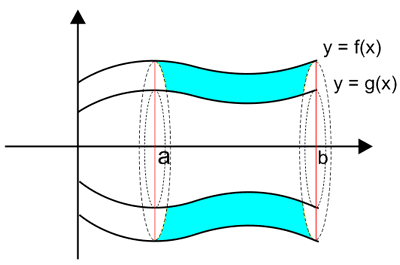
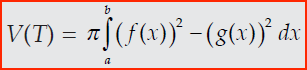
Untuk mencari volume benda putar yang dihasilkan dari sebuah luasan uang diputar menurut sumbu x dan y bisa menggunakan cara seperti penjelasan berikut ini :
a. Volume benda putar terhadap sumbu x yang di batasi 1 kurva
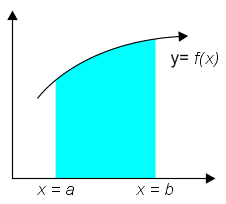
Perhatikan gambar ilustrasi di atas tersebut. Luasan di bawah kurva y=f(x) bila diputar dengan sumbu putar dengan titik batas a dan bmaka akan menghasilkan sebuah silinder dengan tinggi selisih b dan a. Volume benda putar menurut sumbu x tersebut bisa dicari dengan rumus
.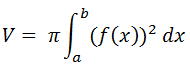
CONTOH SOAL VOLUME BENDA PUTAR TERHADAP SUMBU X
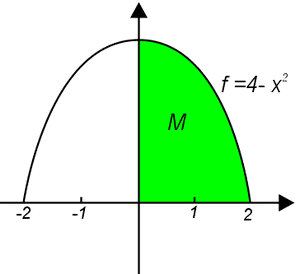
Tentukan volume dari benda putar bila daerah yang dibatasai oleh fungsi f(x) = 4 -x2, sumbu x, dan sumbu y diputar 360º terhadap: Sumbu X
Jawab
1. Diputar mengelilingi sumbu x
Berdasarkan grafik diatas terlihat bahwa luasan r dibatasi oleh titik di sumbu x (0,0) dan (0,2)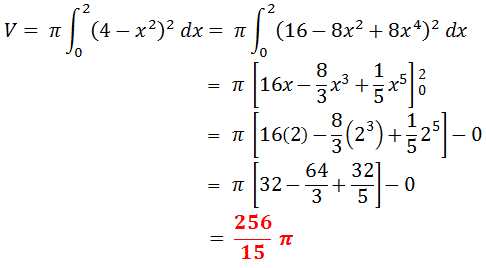
Maka volume benda putar jika luasan M diputar mengelilingi sumbu x sebesar 360% ialah 256/15 π
b. Volume benda putar terhadap sumbu y yang dibatasi 1 kurva
Untuk volume benda putar dengan sumbu putar ialah sumbu y, kalian harus mengubah persamaan grafik yang semula y yang merupakan fungsi dari x menjadi kebalikannya x menjadi fungsi dari y. perhatikan rumus berikut ini:
y = f(x) menjadi x = f(y)
misalkan:
y = x2
x = √y
Setelah persamaan diubah ke bentuk x = f(y) kemudian dimasukkan ke rumus berikut:
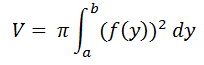
CONTOH SOAL VOLUME BENDA PUTAR TERHADAP SUMBU Y
Tentukan volume dari benda putar bila daerah yang dibatasai oleh fungsi f(x) = 4 -x2, sumbu x, dan sumbu y diputar 360º terhadap: Sumbu y

Diputar mengelilingi sumbu y
Untuk mencari volume benda putarnya kalian harus menyatakan kurva y = f(x) = 4-x2 menjadi bentuk persamaan x2.
y = 4-x2
x2 = 4-y
Luasan M memotong sumbu y di titik (0,0) dan (0,4)
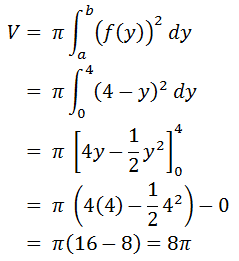
Maka bila luasan M diputar 360º derajat mengelilingi sumbu y akan menghasilkan suatu volume sebesar 8 π satuan volume.






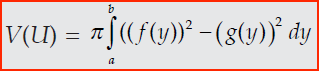
1 Response to "KALKULUS 2 FORUM DISKUSI 16 : VOLUME BENDA PUTAR"
The first is that the vendor must continue to attract cards if his card whole is 16 or less, and he must stand once as} he reaches 17. Remember you can to|you presumably can} initially only see one of many dealer’s cards, so it’s finest follow to assume the dealer’s face-down card is a ten. After every player has been dealt their cards and made 1xbet korea their bets, the vendor then reveals their 2nd card to the table and decides whether or not they want to add an extra card to their hand. Many players appear to hit the wall at 16 and stand regardless of the vendor's up-card. But that 16 is a loser except the vendor busts, and the vendor will make 17 or higher almost eighty p.c of the time with a 7 or higher exhibiting. The danger of busting by hitting 16 is outweighed by the likelihood you will lose when you stand.
Post a Comment