KALKULUS 2 FORUM DISKUSI 15 : INTEGRAL TAK WAJAR

DEFINISI INTEGRAL TAK WAJAR

Dalam kalkulus, integral takwajar adalah limit dari integral tentu dengan batas pengintegralan mendekati bilangan riil tertentu, $-\infty$ , atau gabungan dari beberapa diantaranya. Integral takwajar dinotasikan seperti integral tentu, namun dengan batas pengintegralan tak hingga.

Dengan kata lain, integral tak wajar adalah limit dengan bentuk

$\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx,\qquad \lim _{a\to -\infty }\int _{a}^{b}f(x)\,dx,$

atau

$\lim _{c\to b^{-}}\int _{a}^{c}f(x)\,dx,\quad \lim _{c\to a^{+}}\int _{c}^{b}f(x)\,dx,$

dengan limit diambil pada salah satu atau kedua batasnya. (Apostol 1967, §10.23).

Integral takwajar sering digunakan untuk menghitung nilai integral yang tidak ada dalam arti konvensional (misalnya sebagai integral Riemann), karena adanya singularitas pada fungsi yang hendak diintegralkan, atau salah satu batas adalah tak hingga.

CONTOH INTEGRAL TAK WAJAR

Integral Riemann tidak dapat didefinisikan untuk fungsi $1/{x^{2}}$ pada interval [1, ∞). Hal ini karena domain integral tersebut memiliki domain integrasi tak terbatas. Meskipun demikian, integral Riemann dapat memiliki nilai sebagai integral takwajar dengan menafsirkannya sebagai limit

$\lim _{b\to \infty }\int _{1}^{b}{\frac {1}{x^{2}}}\,dx=\lim _{b\to \infty }\left[-{\frac {1}{b}}+{\frac {1}{1}}\right]=1.$

Integral Riemann juga tidak dapat didefinisikan untuk fungsi $1/{\sqrt {x}}$ pada interval [0, 1] karena integran tak terbatas pada domain integrasi. Meskipun demikian, integral tersebut dapat ditafsirkan sebagai limit

$\lim _{a\to 0^{+}}\int _{a}^{1}{\frac {1}{\sqrt {x}}}\,dx=\lim _{a\to 0^{+}}\left[2{\sqrt {1}}-2{\sqrt {a}}\right]=2.$

DEFINISI INTEGRAL TAK WAJAR SEBAGAI LIMIT JUMLAH RIEMANN

Contoh : Periksa kekonvergenan Integral tak wajar berikut ini

Penyelesaian:

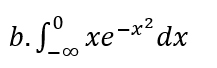
Penyelesaian:

INTEGRAL TAK WAJAR DENGAN INTEGRAN TAK KONTINU

Konvergensi integral

Integral yang tidak tepat menyatu jika batasan yang menentukannya adanya. Dengan demikian contohnya seorang mengatakan bahwa integral tak wajar pada nilai

$\lim _{t\to \infty }\int _{a}^{t}f(x)\,dx$

ada dan sama dengan L jika integral di bawah batas untuk semua cukup besar t, dan nilai limitnya sama dengan L.

Hal ini juga mungkin untuk integral yang tidak tepat untuk menyimpang hingga tak terbatas. Dalam hal ini, seseorang dapat menetapkan nilai dari ∞ (atau -∞) ke integral. Contohnya

$\lim _{b\to \infty }\int _{1}^{b}{\frac {1}{x}}\,dx=\infty .$

Namun sedemikian, integral tidak tepat lainnya mungkin hanya menyimpang ke arah tertentu, seperti nilai

$\lim _{b\to \infty }\int _{1}^{b}x\sin(x)\,dx,$

yang tidak ada, bahkan sebagai bilangan riil diperpanjang Ini disebut divergensi dengan osilasi.

Batasan dari teknik integral yang tidak tepat adalah batasan tersebut harus diambil sehubungan dengan satu titik akhir pada satu waktu. Jadi, integral tak wajar dari bentuk

$\int _{-\infty }^{\infty }f(x)\,dx$