KALKULUS 2 FORUM DISKUSI 3 INTEGRAL TENTU : SOAL DAN PEMBAHASAN INTEGRAL TENTU
DEFINISI INTEGRAL TENTU
Integral tentu didefinisikan sebagai jumlahan suatu daerah yang dibatasi kurva atau persamaan tertentu.
Berbeda dari integral tak tentu, integral tentu memiliki nilai tertentu karena batas yang ditentukan sudah jelas.
Secara umum, integral tentu didefinisikan sebagai
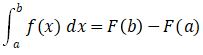
Keterangan:
- f(x) : persamaan kurva
- a, b : batas bawah dan batas atas integral
- F(b), F(a) : nilai integral untuk x = b dan x = a.
PERBEDAAN INTEGRAL TENTU DENGAN INTEGRAL TAK TENTU
1. Integral tertentu memiliki batas bawah dan batas atas, sedangkan integral tak tentu tidak memiliki batas integralnya.
2. Integral tertentu hasilnya biasanya berupa bilangan (tergantung batasnya), sedangkan integral tak tentu hasilnya adalah fungsi
SIFAT-SIFAT PADA INTEGRAL TENTU
Integral sebenarnya dapat ditentukan dengan mudah. Untuk mempermudah perhitungan integral, Gengs dapat memanfaatkan sifat-sifat integral berikut ini.
Pertama. Jika batas atas dan batas bawah dalam suatu integral tentu adalah sama, maka hasil integral tentu dari fungsi tersebut akan sama dengan nol karena tidak ada daerah antara batas batas tersebut.
Berikut ini adalah rumus secara matematis:
Kedua. Jika batas atas dan batas bawah dalam integral tentu diubah posisinya (batas atas menjadi batas bawah dan batas bawah menjadi batas atas) untuk fungsi integral yang sama, maka akan diperoleh hasil hasil yang sama namun berbeda tanda.
Berikut ini adalah rumus secara matematis:
Ketiga. Jika f(x) adalah fungsi integral dan k merupakan tetapan (konstanta) sembarang.
Berikut ini adalah rumus secara matematis:
Keempat. Misalkan diberikan dua buah fungsi yaitu f(x) dan g(x), maka integral tentu dari penjumlahan atau pengurangan kedua fungsi tersebut dapat diselesaikan.
Berikut ini adalah rumus secara matematis:
RUMUS-RUMUS INTEGRAL TENTU
Andaikan f(x) dan g(x) masing-masing adalah fungsi-fungsi kontinyu dan terdefinisi dalam [a,b] dan andaikan k adalah konstanta, maka:
SOAL DAN PEMBAHASAN INTEGRAL TENTU
Soal 1
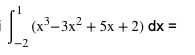
Dalam soal ini, batas atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah melakukan integral fungsi 3x2 + 5x + 2 menjadi seperti di bawah ini.
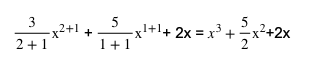
Setelah kita mendapatkan bentuk integral dari fungsi tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut lalu mengurangkannya menjadi seperti berikut.
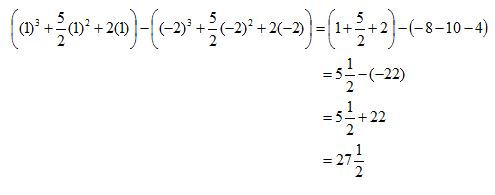
Hasil dari integral tersebut adalah 27,5.
Soal 2.
Carilah hasil dari ʃ21 6x2 dx !
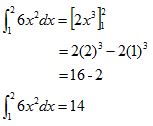
Jadi, hasil dari ʃ21 6x2 dx adalah 14.
3. Berapakah nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx ?
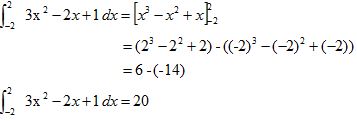
Jadi, nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx adalah 20.
Soal 4.
Hitunglah nilai integral tentu dari ʃ94 1/√x dx !
Jadi, nilai integral tentu dari ʃ94 1/√x dx adalah 2.
Soal 5
Hitunglah hasil dari integral tentu berikut ini
Jawab:
Soal 6
Tentukan hasil integral dari fungsi berikut:
Jawab:
Soal 11
Tentukan !
Jawab:
Kita memiliki fungsi f(x) = 3x2.
Dengan definite integral, maka kita akan memperoleh (kalau integral tak tentu harus ditambah C, sedangkan integral tentu gak ditambah C).
Rumus integral tak tentu
Lalu, kita substitusikan batas atas dan bawahnya ke dalam hasil f(x) = x3.
Batas atas = 2 –> f(2) = 23 = 8.
Batas bawah = 1 –> f(1) = 13 = 1.
Maka, = f(2) – f(1) = 8 – 1 = 7.
Soal 12
Kita lanjut ke contoh soal integral tentu yang kedua.
Tentukan !
Jawab:
Dengan menggunakan rumus axndx dan langsung disubstitusi batas atas dan bawahnya, maka diperoleh hasil sebagai berikut:
Jadi, hasil dari adalah
.
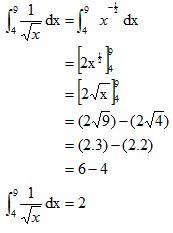
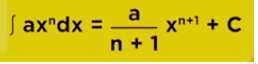
0 Response to "KALKULUS 2 FORUM DISKUSI 3 INTEGRAL TENTU : SOAL DAN PEMBAHASAN INTEGRAL TENTU"
Post a Comment