KALKULUS 2 FORUM DISKUSI 4: INTEGRAL SUBTITUSI DAN INTEGRAL PARSIAL

Rumus Integral Substitusi

Pada bagian awal sudah disinggung sedikit tentang ciri-ciri soal integral yang dapat diselesaikan menggunakan rumus integral substitusi. Intinya, ciri-ciri soal integral yang dapat diselesaikan menggunakan rumus integral substitusi mempunyai faktor yang merupakan turunan dari faktor lainnya.

Perhatikan salah satu contoh soal integral yang dapat diselesaikan menggunakan rumus integral substitusi di bawah.

Contoh Soal yang Dapat Dikerjakan dengan Integral Substitusi

Pengerjaan soal integral seperti di atas membutuhkan teknik dan metode yang tepat untuk mendapatkan hasil integralnya. Metode yang tepat untuk menyelesaikan soal integral di atas adalah rumus integral substitusi. Sebelum mempelejarai cara menyelesaikan soal integral di atas, simak terlebih dahulu persamaan integral substitusi.

Rumus integral substitusi diberikan melalui persamaan di bawah.

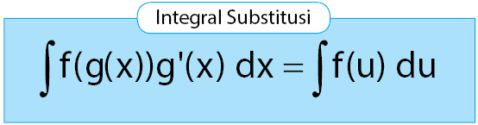
Sekarang, mari kita coba selesaikan soal integral yang telah diberikan sebelumnya menggunakan persamaan di atas. Perhatikan proses perngerjaan yang diberikan di bawah.

Perhatikan kembali soal integral yang diberikan!

integral substitusi

Turunan dari x2 ‒ 4 adalah 2x,
dengan demikian, dapat menduga bahwa soal integral di atas dapat diselesaikan menggunakan rumus integral substitusi.

Perhatikan langkah-langkah untuk menggunakan rumus integral substitusi seperti pada cara berikut.

Misalkan:
u = x2 ‒ 4
du/dx = 2x → dx = du/2x

Sehingga, penyelesaian bentuk soal dengan menggunakan rumus integral substitusi dapat dilakukan seperti cara berikut.

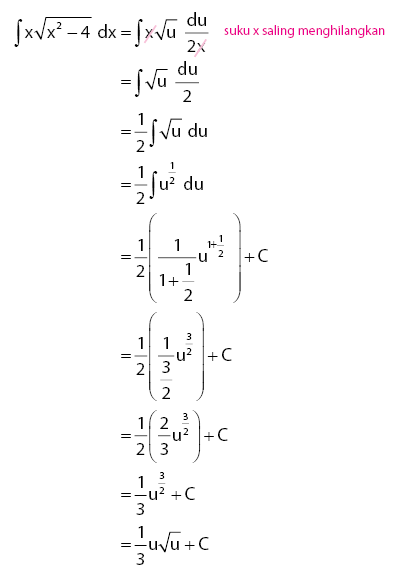
Setelah mendapatkan hasil akhir dalam persamaan u, perlu mengembalikan kembali pemisalan u = x2 ‒ 4 yang dilakukan di awal. Sehingga, dapat diperoleh hasil seperti berikut.

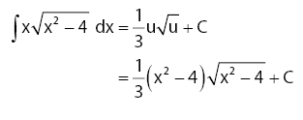
rumus integral substitusi

INTEGRAL SUBSITUSI SEBAGAI METODE TEKNIK INTEGRAL

Integral Substitusi adalah metode penyelesaian masalah melalui integral dengan cara substitusi kepada bentuk yang lebih sederhana, bentuk sederhana yang dimaksud adalah berkaitan dengan turunan suatu variabel.

Merubah dari bentuk yang belum dikenal menjadi lebih mudah dikenal atau bentuk primitifnya.

Untuk lebih memahami, perhatikanlah contoh soal integral substitusi dan pembahasannya berikut:

Soal dan Pembahasan - Integral Substitusi - 1

Soal dan Pembahasan - Integral Substitusi - 2

INTEGRAL SUBSITUSI PADA FUNGSI ALJABAR

Ciri-ciri soal yang bisa diselesaikan dengan rumus integral substitusi ialah memiliki faktor turunan dari faktor lainnya. Sedangkan teknik integral substitusi pada fungsi aljabar yaitu f(x) bisa diubah dalam bentuk k.(g(x))n.gI(x).

Perhatikan jika U= g(x) maka

(x) atau dU= gI(x) .dx

Jika

Maka integral tersebut bisa diselesaikan dengan memisalkan U= g(x) serta U= gI(x) dx sehingga akan diperoleh persamaan sebagai berikut:

Hal tersebut berlaku dengan n ≠–1.

Namun apabila n = -1, sehingga akan diperoleh:

. dU = 1n U + C

CONTOH SOAL DAN PEMBAHASAN INTEGRAL SUBSITUSI

contoh soal dan pembahasan integral subtitusi :

1. $\int (5x-3)^4dx=....$

Jawab :

* kita misalkan u=5x-3

dan fungsi u dapat diturunkan menjadi

$\begin{align*}{\color{Red} u}&=&{\color{Red} 5x-3}\\\frac{du}{dx}&=&5\\dx&=&{\color{Blue} \frac 15\;du} \end{align*}$

* Baru kita subtitusikan ke soal :

$\begin{align*}\int({\color{Red} 5x-3})^4{\color{Blue} dx}&=&\int {\color{Red} u}^4.{\color{Blue} \frac 15\;du}\\&=&{\color{Blue} \frac 15}.\frac{1}{4+1}.{\color{Red} u}^{4+1}+C\\&=&\frac{1}{25}\;{\color{Red} u}^5+C\\&=&\frac{1}{25}\;({\color{Red} 5x-3})^5+C\end{align*}$

Jangan sampai lupa untuk mengembalikan permisalan kita $u={\color{Red} 5x-3}$ ya…..

2. $\int (2x-1)(3x^2-3x+5)^8\;dx=...$

Jawab :

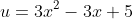* kita misalkan u=3x^2-3x+5

dan fungsi u dapat diturunkan menjadi :

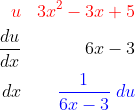
$\begin{align*}{\color{Red} u}&=&{\color{Red} 3x^2-3x+5}\\\frac {du}{dx}&=&6x-3\\dx&=&{\color{Blue} \frac{1}{6x-3}\;du}\end{align*}$

* Baru kita subtitusikan ke soal :

$\begin{align*}\int (2x-1)(3x^2-3x+5)^8\;dx&=&\int (2x-1).{\color{Red} u}^8\;{\color{Blue} \frac{1}{6x-3}\;du}\\&=&\int \frac{2x-1}{{\color{Blue} 3(2x-1)}}\;{\color{Red} u}^8\;{\color{Blue} du}\\&=&\int \frac{1}{3}\;{\color{Red} u}^8\;{\color{Blue} du}\\&=&\frac 13.\frac{1}{8+1}.{\color{Red} u}^{8+1}+C\\&=&\frac{1}{27}.{\color{Red} u}^9 +C\\&=&\frac{1}{27}({\color{Red} 3x^2-3x+5})^9+C\end{align*}$

3. $\int x^2\sqrt{2x^3+1}\;dx=...$

Jawab :

* kita misalkan u=2x^3+1

dan fungsi u dapat diturunkan menjadi

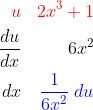
$\begin{align*}{\color{Red} u}&=&{\color{Red} 2x^3+1}\\\frac{du}{dx}&=&6x^2\\dx&=&{\color{Blue} \frac{1}{6x^2}\;du} \end{align*}$

* Baru kita subtitusikan ke soal :

$\begin{align*}\int x^2\sqrt{2x^3+1}\;dx&=&\int x^2.\sqrt{{\color{Red} u}}\;.{\color{Blue} \frac{1}{6x^2}\;du}\\&=&\int \frac{x^2}{{\color{Blue} 6x^2}}.{\color{Red} u}^{\frac 12}\;{\color{Blue} du}\\&=&\int \frac{1}{6}.{\color{Red} u}^{\frac 12}\;{\color{Blue} du}\\&=&\frac 16.\frac{1}{\frac 12+1}\;{\color{Red} u}^{\frac 12+1}+C\\&=&\frac 16.\frac 23\;{\color{Red} u}^{\frac 32}+C\\&=&\frac 19\;{\color{Red} u}\sqrt {\color{Red} u}+C\\&=&\frac 19({\color{Red} 2x^3+1})\sqrt{{\color{Red} 2x^3+1}}+C\end{align*}$

SOAL-SOAL INTEGRAL SUBSITUSI FUNGSI ALJABAR

Jika f(x) = (x4+5)3x3, untuk memperoleh integralnya yaitu dengan memisalkan: x4+5 = U serta = 4x3, sehingga x3 dx = 1/4 dU .

Berdasarkan pemisalan di atas, sehingga persamaan intergralnya yaitu:

Apabila hasil diatas kemudian disubstitusikan dengan permisalan U maka akan diperoleh:

Contoh di atas adalah tehnik substitusi untuk integral tak tentu. Pada suatu kasus integral tertentu, dimana pada nilai interval a≤ b ≤c tertentu, sehingga intervalnya harus disubstitusi dalam interval baru bagi variabel U. contohnya f02 (x4 + 5)3 x3 dx, dengan pemisalan:

X4 + 5= U dan , sehingga x3 dx= Agar persamaan integral dalam U bisa tercipta, maka interval 0≤ x ≤2 diubah menjadi:

X=0 → U= x4+5 = 04= 5= 5
X=2 → U= x4+5 =24+5 =21

Dari permisalan di atas, maka persamaan integralnya yaitu:

Soal No. 1
Tentukan:

∫ (3x + 7)5 dx

Pembahasan

Bawa ke bentuk ∫ vn dv
Misal:
v = (3x + 5) dengan demikian:

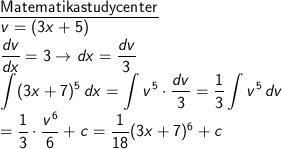
Soal No. 2

Tentukan dengan menggunakan metode substitusi aljabar :

∫ (2x + 10)3 dx

Pembahasan

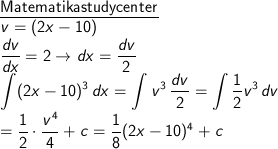
Soal No. 3

Tentukan hasil dari:

∫ √(3x + 6) dx

Pembahasan

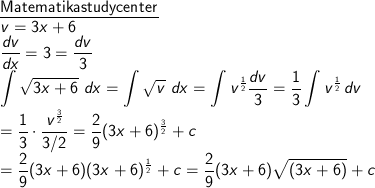
Soal No. 4
Tentukan hasil dari:

∫ 3√(3x + 6) dx

Pembahasan

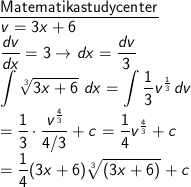
Soal No. 5
Tentukan hasil dari:

∫ (3x3 + 5)7 x2 dx

Pembahasan

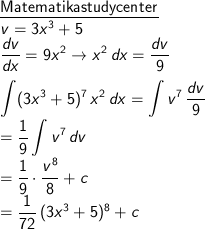
Soal No. 5
Tentukan hasil dari:

∫ 3√(12 x5 − 7) x4 dx

Pembahasan

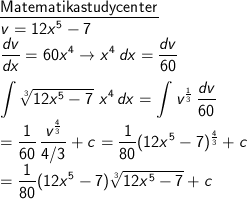
Soal No. 7
Hasil dari

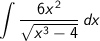
adalah….

Pembahasan

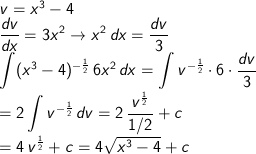
Pengertian Integral Parsial

Integral parsial adalah teknik pengintegralan dengan cara parsial. Apa itu teknik parsial? Teknik parsial adalah teknik penyelesaian integral dengan cara pemisalan karena komponen yang diintegralkan memuat variabel yang sama namun berbeda fungsi. Biasanya, integral parsial ini digunakan untuk menyelesaikan persamaan yang cukup komplek. Bentuk umum integral parsial adalah sebagai berikut.

Adapun keterangan masing-masing variabel adalah sebagai berikut.

u = f(x), sehingga du = f(x)dx

dv = g(x)dx, sehingga v = g(x)dx

Jika f(x) berupa polinom derajat n ≥ 1, n ∈ asli, maka bentuk formula di atas bisa disederhanakan seperti skema berikut.

Tabel di atas menunjukkan bahwa, kolom fungsi f(x) di sebelah kiri merupakan fungsi yang harus diturunkan sampai turunannya bernilai 0. Sementara itu, kolom fungsi g(x) sebelah kanan harus diintegralkan sampai kolom sebelah kiri bernilai 0. Ketentuan lainnya adalah tanda fungsinya selalu beselang-seling, yaitu dari positif (+) menjadi negatif (–) dan seterusnya.

Dengan demikian, bentuk integralnya bisa dituliskan sebagai berikut.

PENYELESAIAN DENGAN CARA TEKNIK PARSIAL

Contoh Soal 1

Tentukan hasil integral dari persamaan berikut.

Pembahasan:

Pertama, kamu harus membuat permisalan seperti pada pembahasan sebelumnya. Jika dalam memisalkan kamu menemukan adanya pangkat 2 (polinom derajat 2), gunakan cara skema agar pengerjaan menjadi lebih cepat.

Misal, u = x2 polinom derajat 2. Dengan demikian, akan lebih mudah menggunakan cara skema seperti berikut.

Contoh Soal 2

Tentukan hasil integral dari persamaan berikut.

Pembahasan:

Bentuk soal di atas diselesaikan dengan metode dasar karena tidak mengandung polinom derajat bilangan asli.

dv = dx, maka v = x

Kemudian, gunakan cara berikut.

Jadi, hasil integral dari adalah xInx – x + c.

TEKNIK INTEGRAL SUBSITUSI METODE PARSIAL

Tidak semua integral dapat diselesaikan dengan menggunakan metode integral substitusi untuk menyelesaikan integral tersebut kita bisa menggunakan alternatif metode integral parsial. Untuk memahami tentang integral parsial perhatikan penjelasan berikut.
Misalkan y = uv
maka y' = u'v + uv' atau

$\frac{dy}{dx}=\frac{du}{dx}v+u\frac{dv}{dx}$

Jika ruas kiri terhadap ruas kanan diintegralkan terhadap x, diperoleh

$\int dy=\int vdu+\int udv$

$y=\int vdu+\int udv$
Karena y = uv maka,

$uv=\int vdu+\int udv$
sehingga

$\int udv=uv-\int vdu$
Untuk lebih memahami penggunaan dari metode integral parsial, perhatikan contoh berikut.
Selesaikan integral $\int x(x-3)^{4}dx$ !
Penyelesaian:
Misalkan
u = x <---> du = dv
dv = (x - 3)4 dx <---> $v = \int (x-3)^{4}dx = \frac{1}{5}(x-3)^{5}$

$\int x(x-3)^{4}dx = x\frac{1}{5}(x-3)^{5}-\int \frac{1}{5}(x-3)^{5}$
   $= \frac{1}{5}x(x-3)^{5}-\frac{1}{5}\cdot \frac{1}{6}(x-3)^{6}+C$
   $= (\frac{1}{5}x-\frac{1}{30}(x-3))(x-3)^{5}+C$
   $= (\frac{1}{5}x-\frac{1}{30}x-\frac{3}{30})(x-3)^{5}+C$
   $= \frac{1}{30}(5x-3)(x-3)^{5}+C$
Selain pada integral tak tentu, teknik integral parsial juga dapat digunakan pada integral tertentu.

TEKNIK INTEGRAL PARSIAL BILA SUBSITUSI TIDAK MEMBERI SOLUSI

Apabila pengintegralan dengan teknik atau metode substitusi tidak berhasil, maka teknik pengintegralan lain mungkin dapat memberikan hasil. Teknik pengintegralan yang akan kita bahas di sini dikenal dengan teknik pengintegralan parsial. Teknik ini didasarkan pada pengintegralan rumus turunan hasil kali dua fungsi.

Andaikan u=u(x) dan v=v(x). Maka

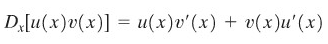
atau

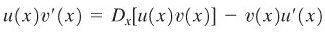
Dengan mengintegralkan dua ruas persamaan tersebut, kita peroleh

Persamaan terakhir ini dapat kita tuliskan untuk integral tentu dan tak tentu.

Pengintegralan Parsial: Integral Tak Tentu dan Integral Tentu

Karena dv=v′(x) dx dan du=u′(x) dx, maka untuk integral tak tentu, pengintegralan parsial dapat dituliskan sebagai

Sedangkan rumus pengintegralan parsial untuk integral tentu adalah

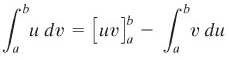
Rumus di atas memungkinkan kita memindahkan masalah pengintegralan u dvu dv pada pengintegralan v duv du. Pengintegralan terakhir ini tergantung pada pemilihan uu dan dvdv yang tepat.

Gambar 1 di bawah mengilustrasikan interpretasi geometrik untuk pengintegralan parsial.

KALKULUS 2 FORUM DISKUSI 4: INTEGRAL SUBTITUSI DAN INTEGRAL PARSIAL

INTEGRAL SUBSITUSI SEBAGAI METODE TEKNIK INTEGRAL

INTEGRAL SUBSITUSI PADA FUNGSI ALJABAR

CONTOH SOAL DAN PEMBAHASAN INTEGRAL SUBSITUSI

SOAL-SOAL INTEGRAL SUBSITUSI FUNGSI ALJABAR

PENYELESAIAN DENGAN CARA TEKNIK PARSIAL

Contoh Soal 1

Contoh Soal 2

TEKNIK INTEGRAL SUBSITUSI METODE PARSIAL

TEKNIK INTEGRAL PARSIAL BILA SUBSITUSI TIDAK MEMBERI SOLUSI

Pengintegralan Parsial: Integral Tak Tentu dan Integral Tentu

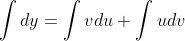
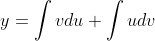
0 Response to "KALKULUS 2 FORUM DISKUSI 4: INTEGRAL SUBTITUSI DAN INTEGRAL PARSIAL "

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel