KALKULUS 2 FORUM DISKUSI 5 : INTEGRAL FUNGSI TRIGONOMETRI

Integral fungsi trigonometri dapat diperoleh dengan mudah berdasarkan informasi bahwa integral merupakan anti turunan atau kebalikan dari turunan, yakni

∫Dx(f(x)) dx=f(x)

Kita tahu bahwa ketika suatu fungsi, katakanlah fungsi f(x), diturunkan atau didiferensialkan maka akan diperoleh suatu fungsi baru, katakanlah f'(x). Jika fungsi baru hasil turunan dari f(x) diintegralkan, maka kita akan memperoleh fungsi f(x) itu sendiri.

Perhatikan Tabel 1 berikut yang menunjukkan turunan dari beberapa fungsi trigonometri dan integralnya dengan memanfaatkan informasi bahwa integral merupakan suatu anti turunan.

Tabel 1. Fungsi f(x), turunannya dan anti turunan atau integral tak tentu dari fungsi f(x)

No	Fungsi f(x) = y	Turunan: dy/dx	Integral
1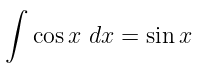
2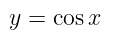
3
4
5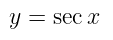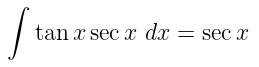
6

CONTOH SOAL INTEGRAL SUBSITUSI FUNGSI TRIGONOMETRI

CONTOH 1:

Penyelesaian:

Misalkan u=3√x−4   , maka u3=x−4  dan 3u2 du=dx . Dengan demikian, kita peroleh

CONTOH 2:

Penyelesaian:

Misalkan u=(x+1)1/5  , maka u5=x+1  dan  5u4 du=dx . Dengan demikian, kita peroleh

TEKNIK INTEGRAL SUBSTITUSI TRIGONOMETRI

Teknik integral yang akan kita bahas yaitu teknik integral substitusi trigonometri. Dengan substitusi trigonometri yang tepat bentuk akar dalam integran dapat dirasionalkan dan karena itu dapat dengan mudah untuk diintegralkan.

Integran yang mengandung √(a2−x2),√(a2+x2) , dan √(x2−a2)

Apabila kita menjumpai integran yang fungsinya mengandung ketiga bentuk akar di atas, maka teknik integral substitusi trigonometri dapat diterapkan. Untuk merasionalkan bentuk akar-akar tersebut kita gunakan substitusi berikut:

Dari substitusi tersebut, kita peroleh hasil berikut:

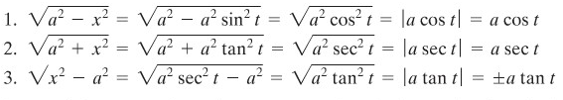
Perhatikan bahwa pembatasan pada tt memungkinkan kita untuk menghilangkan tanda nilai absolut pada dua kasus pertama. Selain itu, pembatasan ini juga membuat fungsi sin,tansin,tan dan secsec menjadi dapat diinverskan.

SUBSITUSI TRIGONOMETRI INTEGRAL BENTUK AKAR

Substitusi trigonometri dapat digunakan untuk menyelesaikan integral yang memuat bentuk akar

Tujuan dari penggunaan substitusi trigonometri adalah untuk menghilangkan akar tersebut dalam integran. Kita dapat melakukan hal ini dengan menggunakan identitas Pythagoras

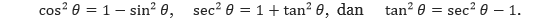
Sebagai contoh, jika a > 0, misalkan u = a sin θ, dengan –π/2 < θ < π/2. Maka

Perhatikan bahwa cos θ ≥ 0, karena –π/2 < θ < π/2.

Substitusi Trigonometri

1. Untuk integral yang memuat √(a² – u²), misalkan u = a sin θ. Maka, didapatkan √(a² – u²) = a cos θ, di mana –π/2 < θ < π/2.
   
2. Untuk integral yang memuat √(a² + u²), misalkan u = a tan θ.
   Maka, √(a² + u²) = a sec θ, dengan –π/2 < θ < π/2.
   
3. Untuk integral yang memuat √(u² – a²), misalkan u = a sec θ. Maka,
   
   

Catatan Batasan dari θ memastikan bahwa fungsi pada substitusi tersebut merupakan fungsi satu-satu. Faktanya, batasan tersebut merupakan interval yang sama di mana arcsinus, arctangen, dan arcsecan didefinisikan.

CONTOH SUBSTITUSI TRIGONOMETRI

CONTOH 

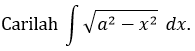
Penyelesaian:

Untuk menyelesaikan soal ini kita gunakan substitusi berikut:

sehingga kita peroleh dx=acost dtdx=acos⁡⁡t dt dan √a2−x2=acosta2−x2=acos⁡⁡t. Dengan demikian,

Oleh karena x=asintx=asin⁡t ekivalen dengan x/a=sintx/a=sin⁡⁡t dan oleh karena selang tt kita batasi sehingga sinus memiliki invers, maka

Dan dengan sebuah kesamaan yang telah kita pelajari mengenai fungsi trigonometri, kita peroleh

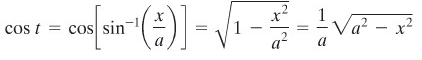
Ini dapat pula dilihat pada Gambar 1 di bawah ini.

Gambar 1.

Dengan demikian,

SUBSITUSI TRIGONOMETRI u = a sin θ

Contoh 1: Substitusi Trigonometri: u = a sin θ

Selesaikan,

Pembahasan Untuk menggunakan substitusi trigonometri, kita harus melihat bahwa √(9 – x²) merupakan bentuk dari √(a² – u²). Sehingga kita dapat menggunakan substitusi

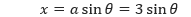
Sehingga, persamaan yang menghubungkan variable x dan θ di atas dapat dimodelkan ke dalam segitiga siku-siku sebagai berikut.

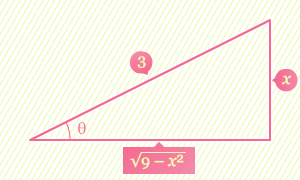
Dengan menggunakan turunan dan segitiga di atas, kita mendapatkan

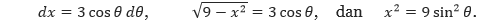
Sehingga, dengan menggunakan substitusi dihasilkan

 

Perhatikan bahwa segitiga pada gambar di pembahasan Contoh 1 tersebut, dapat juga digunakan untuk mengubah θ kembali menjadi x sebagai berikut.

Contoh 2: Substitusi Trigonometri: u = a tan θ

Tentukan,

 

Pembahasan Misalkan u = 2x, a = 1, dan 2x = tan θ, seperti yang dapat digambarkan sebagai berikut.

Sehingga, kita mendapatkan

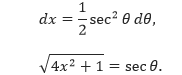
Dengan menggunakan substitusi trigonometri, didapatkan

Selanjutnya kita dapat memperluas penggunaan dari substitusi trigonometri untuk menyelesaikan integral yang memuat bentuk (a² – u²)n/2 dengan menuliskan bentuk tersebut ke dalam

Share this post