KALKULUS 2 FORUM DISKUSI 6 : INTEGRAL EKSPONEN
MENGENAL BENTUK INTEGRAL EKSPONEN
Bentuk integral eksponen yang pertama kali harus kita ketahui adalah

dengan e adalah bilangan natural yang besarnya
e =2,71828182845904523….
Terkadang ex biasa ditulis menjadi exp (x)
Jadi
∫exp (x) dx = exp (x) + c
Bagaimana jika bilangan pokoknya bukan e ?

Dengan a adalah bilangan positif
Sedangkan ln a = elog a
Oleh sebab itu kita tidak perlu menuliskan

karena ln e = elog e = 1
Integral Eksponensial
Fungsi eksponensial biasanya dinotasikan dengan ex. Beberapa konsep dasar yang harus dipelajari dalam integral eksponensial yaitu
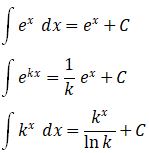
Keterangan:
- ex, ekx : fungsi eksponensial
- C : konstanta
RUMUS INTEGRAL FUNGSI EKSPONEN
Suatu logaritma dengan basis e dinamakan logaritma natural dan ditulis dengan ln. Sehinga
Untuk mendapatkan integral bentuk eksponen dan logaritma, perlu diketahui turunannya terlebih dahulu yaitu
Pengembangan dari rumus diatas adalah dengan menggunakan aturan substitusi dan parsial.
SOAL DAN PEMBAHASAN INTEGRAL SUBSITUSI FUNGSI EKSPONEN
ungsi Eksponensial adalah Fungsi yang biasa dinotasikan dalam bentuk e^x (e pangkat x), dimana e adalah basis logaritma natural.
Dalam mengintegralkan fungsi eksponensial, ada 2 rumus dasar yang harus dipahami.
Perhatikan pembahasan 2 soal berikut ini.
CONTOH INTEGRAL EKSPONENSIAL FUNGSI ALJABAR
CONTOH :

Penyelesaian:
Ingatlah bentuk baku ∫1/(a2+u2)du. Andaikan u=3eX, maka du=3eX dx. Sehingga
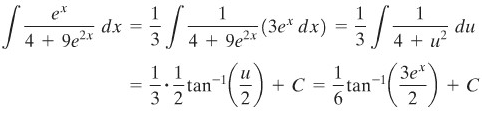
CONTOH SOAL INTEGRAL FUNGSI EKSPONEN
Contoh soal 1 :

Jawab :
misal y = 5x + 3
maka

Jadi

Contoh soal 2 :

Jawab :
misal y = x2 + 6x + 7
maka




Contoh Soal 3 :

Jawab :
Misalkan y = sin x
maka







INTEGRAL FUNGSI EKSPONEN SUBSITUSI ALJABAR
Contoh Soal 4 :

Jawab :
Misalkan y = ex
Maka 
sehingga 
Jadi






Contoh Soal 5 :

Jawab :
Misalkan y = ex + 5
Maka 
sehingga 
Jadi





Contoh Soal 6 :

Jawab :
Misal
y = e3x + e –3x
Maka 
sehingga

Jadi





Contoh Soal 7:

Jawab :
Misalkan y = ex – e — x
Maka 
sehingga 
Jadi











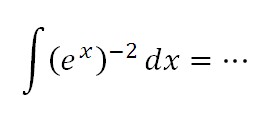





0 Response to "KALKULUS 2 FORUM DISKUSI 6 : INTEGRAL EKSPONEN"
Posting Komentar