KALKULUS 2 FORUM DISKUSI 11

INTEGRAN FUNGSI RASIONAL SIN X DAN COS X

Bila integran merupakan fungsi rasional yang memuat suku-suku dari sin dan cos maka akan lebih mudah bila dikerjakan menggunakan substitusi, yaitu u = tan ( x/2) dengan batas

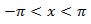
Integran ditransformasikan ke dalam fungsi rasional dari u dan ini dikerjakan sebagaimana metode pecahan parsial di atas. Keseluruhan dari bentuk yang akan disubstitusikan ke dalam integran dapat diperlihatkan seperti di bawah ini.

Dari : u = tan ( x/2 ). Maka :

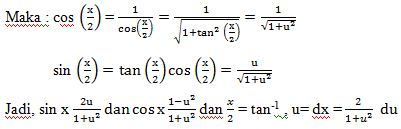
Contoh Soal :

Integrasi fungsi secara rasional bergantung pada fungsi trigonometri

1. Integral bentuk sin n xdx , cos n xdx , n>0
a) Jika n ganjil, maka satu pangkat sinx (atau cosx) harus ditempatkan di bawah tanda diferensial, dan dari sisa pangkat genap, satu harus menuju fungsi yang berlawanan.
b) Jika n genap, maka kita menggunakan rumus reduksi
2. Integral dari bentuk tg n xdx , ctg n xdx , di mana n adalah bilangan bulat.
Rumus harus digunakan

3. Integral bentuk sin n x cos m x dx
a) Misalkan m dan n berbeda paritas. Kami menerapkan substitusi t=sin x jika n ganjil atau t=cos x jika m ganjil.
b) Jika m dan n genap, maka kita menggunakan rumus reduksi
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integral bentuk 
Jika bilangan m dan n memiliki paritas yang sama, maka kita menggunakan substitusi t=tg x . Seringkali lebih mudah untuk menerapkan teknik satuan trigonometri.
5. sin(nx) cos(mx)dx , cos(mx) cos(nx)dx , sin(mx) sin(nx)dx

Mari kita gunakan rumus untuk mengubah produk fungsi trigonometri menjadi jumlah mereka:

• sin cos = (sin(α+β)+sin(α-β))
• cos cos = (cos(α+β)+cos(α-β))
• sin sin = (cos(α-β)-cos(α+β))
• 
  

CONTOH SOAL INTEGRAL COS X DAN SIN X

Contoh
1. Hitung integral cos 4 x sin 3 xdx .
Kami membuat substitusi cos(x)=t . Maka cos 4 x sin 3 xdx = 
2. Hitung integralnya.
Membuat substitusi sin x=t , kita dapatkan

3. Temukan integralnya.
Kami membuat penggantian tg(x)=t . Mengganti, kita dapatkan
.........

Metode untuk mengintegrasikan fungsi rasional sin x dan cos x

Fungsi rasional dari dosa x dan cos x adalah fungsi turunan dari dosa x, cos x dan konstanta apa pun yang menggunakan operasi penjumlahan, pengurangan, perkalian, pembagian, dan peningkatan ke pangkat bilangan bulat. Mereka dilambangkan sebagai berikut: R (sinx, cosx). Ini juga dapat mencakup garis singgung dan kotatangen, karena mereka dibentuk dengan membagi sinus dengan kosinus dan sebaliknya.
Integral fungsi rasional memiliki bentuk:
.

Metode pengintegrasian fungsi trigonometri rasional adalah sebagai berikut.
1) Substitusi selalu mengarah ke integral dari pecahan rasional. Namun, dalam beberapa kasus, ada substitusi (lihat di bawah) yang menghasilkan perhitungan yang lebih singkat.
2) Jika R (sinx, cosx) cos x → - cos x dosa x.
3) Jika R (sinx, cosx) dikalikan dengan -1 saat mengganti dosa x → - dosa x, maka substitusi t = cos x.
4) Jika R (sinx, cosx) tidak berubah seperti dengan penggantian simultan cos x → - cos x, dan dosa x → - dosa x, maka substitusi t = tg x atau t= ctg x.

Rumus-Rumus Dasar Integral Fungsi Trigonometri

     ∫ sin x dx = −cos x + C
     ∫ cos x dx = sin x + C

     ∫ sec2 x dx = tan x + C
     ∫ csc2 x dx = −cot x + C
     ∫ sec x . tan x dx = sec x + C
     ∫ csc x . cot x dx = −csc x + C

Perluasan Rumus

     ∫ sin ax dx = −1a1acos ax + C
     ∫ sin (ax + b) dx = −1a1acos (ax + b) + C

Untuk fungsi trigonometri lainnya dapat ditentukan dengan mengikuti pola diatas yang tentunya juga harus menyesuaikan dengan rumus dasar

CONTOH SOAL INTEGRAL FUNGSI TRIGONOMETRI

Contoh
a. ∫ sin 3x dx = −1/3−1/3 cos 3x + C

b. ∫ 2 cos(3x + 1) dx = 2/3 sin (3x + 1) + C

c. ∫ 3 sec2 (4x − 1) dx = 3/4 tan (4x − 1) + C

d. ∫ csc 4x . cot 4x dx = −1/4 csc 4x + C

KONSEP TRIGONOMETRI

Berikut beberapa konsep trigonometri yang sering digunakan :

sin A = 1/cscA
cos A = 1/secA
tan A = sinA/cosA
cot A = cosA/sinA

sin2A + cos2A = 1
tan2A = sec2A − 1
cot2A = csc2A − 1

sin 2A = 2 sin A cos A
cos 2A = cos2A − sin2A
cos 2A = 1 − 2sin2A
cos 2A = 2cos2A − 1

sin2A = 1/2−1/2 cos 2A
cos2A = 1/2 +1/2cos 2A

2 sin A cos B = sin (A+B) + sin (A−B)
2 cos A sin B = sin (A+B) − sin (A−B)
2 cos A cos B = cos (A+B) + cos (A−B)
−2 sin A sin B = cos (A+B) − cos (A−B)

Contoh Soal Integral Fungsi Trigonometri

Contoh 1
∫ sin2x dx = ...

Jawab :
⇒ ∫ (12−1212−12cos 2x) dx
= 1212x − 1212. 1212sin 2x + C
= 1212x − 1414sin 2x + C


Contoh 2
∫ (sin 3x − cos 3x)2 dx = ...

Jawab :
⇒ ∫ (sin23x + cos23x − 2 sin 3x cos 3x) dx
⇒ ∫ (1 − sin 2.3x) dx
⇒ ∫ (1 − sin 6x) dx
= x − (−16−16cos 6x) + C
= x + 1616cos 6x + C


Contoh 3
 ∫ (tan24x + 3) dx = ...

Jawab :
⇒ ∫ (sec24x − 1 + 3) dx
⇒ ∫ (sec24x + 2) dx
= 1414tan 4x + 2x + C

Contoh 4
∫ (tan 2x − sec 2x)2 dx = ...

Jawab :
⇒ ∫ (tan22x + sec22x − 2 sec 2x tan 2x) dx
⇒ ∫ (sec22x − 1 + sec22x − 2 sec 2x tan 2x) dx
⇒ ∫ (2sec22x − 2 sec 2x tan 2x − 1) dx
= 2/2 tan 2x − 2/2 sec 2x − x + C
= tan 2x − sec 2x − x + C


Contoh 5
∫ 4 sin 4x cos 2x dx = ...

Jawab :
⇒ ∫ 4/2 [sin (4x+2x) + sin (4x−2x)] dx
⇒ ∫ (2sin 6x + 2sin 2x) dx
= −2/6−2/6cos 6x + (−2/2−2/2cos 2x) + C
= −1/3−1/3cos 6x − cos 2x + C


Contoh 6
∫1−tan2xsec2x∫1−tan2xsec2x dx = ...

Jawab :
⇒ ∫ 1−(sec2x−1)sec2x1−(sec2x−1)sec2x dx
⇒ ∫ 2−sec2xsec2x2−sec2xsec2x dx
⇒ ∫ (2sec2x−sec2xsec2x)(2sec2x−sec2xsec2x) dx
⇒ ∫ (2cos2x − 1) dx
⇒ ∫ cos 2x dx
= 1/2sin 2x + C

Share this post